1.4 L0、L1和L2

衡量一个向量的大小，在机器学习领域通常用范数来衡量。形式上，$$ L^p $$ 范数定义如下：

$$ ||x||_p=(\sum_i|x_i|^p)^{\frac 1 p} $$

L0范数是指向量中非0的元素的个数。

L1范数是指向量中各个元素绝对值之和，也叫为“稀疏规则算子”（Lasso Regularization）。

L2范数不逊于L1范数，它有两个美称，在回归里面，叫“岭回归”（Ridge Regression），也有人叫它“权值衰减weight decay”。 是指向量各元素的平方和然后求平方根。

在正则化应用时【比较】：

• 下降速度：最小化权值参数L1比L2变化得快。
• 模型空间的限制：L1会产生稀疏 L2不会。L1会趋向于产生少量的特征，而其他的特征都是0，方便特征提取。而L2会选择更多的特征，这些特征都会接近于0。
• L2范数可以防止过拟合，提升模型的泛化能力。
• L2对大数，对outlier离群点更敏感。

下面举例说明L1为啥比L2更容易获得稀疏：

假设费用函数 L 与某个参数 x 的关系如图所示：

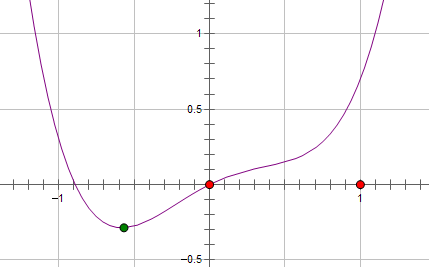
则最优的 x 在绿点处，x 非零。现在施加 L2 regularization，新的费用函数（）如图中蓝线所示：

最优的 x 在黄点处，x 的绝对值减小了，但依然非零。

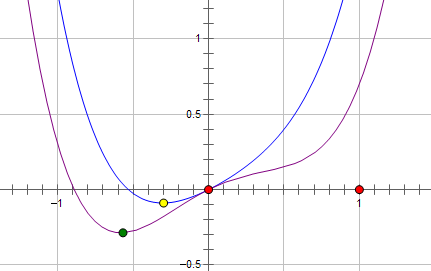
而如果施加 L1 regularization，则新的费用函数（）如图中粉线所示：

最优的 x 就变成了 0。这里利用的就是绝对值函数的尖峰。

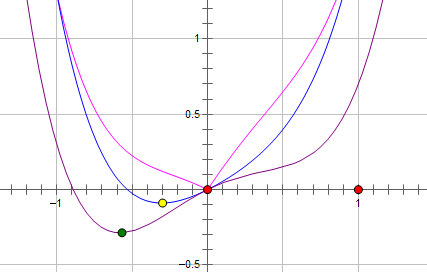
两种 regularization 能不能把最优的 x 变成 0，取决于原先的费用函数在 0 点处的导数。如果本来导数不为 0，那么施加 L2 regularization 后导数依然不为 0，最优的 x 也不会变成 0。而施加 L1 regularization 时，只要 regularization 项的系数 C 大于原先费用函数在 0 点处的导数的绝对值，x = 0 就会变成一个极小值点。

上面只分析了一个参数 x。事实上 L1 regularization 会使得许多参数的最优值变成 0，这样模型就稀疏了。

下图结合L1和L2的公式进行了形象的解释。

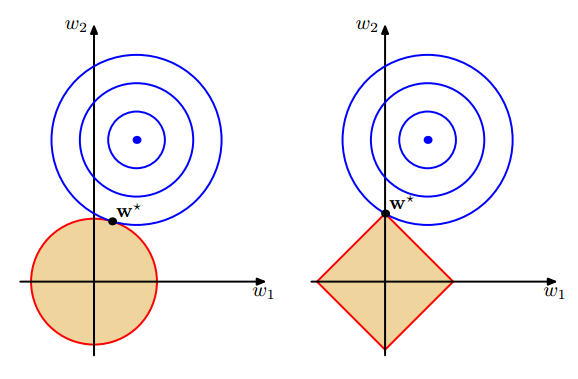
那么稀疏到底有什么好处呢？稀疏表达的意义实际在于降维。

且这个降维并不局限于节省空间。更多地意义在于，在Machine Learning，Signal/Image Processing等众多领域，很多反问题(Inverse Problem)都是不适定/病态的(under-determined, ill-posed)。如

为了能获得比较好的解，人们需要的x先验知识。而稀疏性便是众多先验知识中，最为主要的一种。这种降维主要表现于虽然原始信号x的维度很高，但实际的有效信息集中在一个低维的空间里。这种性质使得不适定的问题变得适定(well-posed)，进而使获得“好的解”成为可能。