1.6.2 交叉熵
从方差代价函数说起
代价函数经常用方差代价函数(即采用均方误差MSE),比如对于一个神经元(单输入单输出,sigmoid函数), 定义其代价函数为:
$$ C= \dfrac {(y-a)^2} 2 $$
其中y 是我们期望的输出,a为神经元的实际输出( a=σ(z), where z=wx+b)。
在训练神经网络过程中,我们通过梯度下降算法来更新w和b,因此需要计算代价函数对w和b的导数:这里假设了神经元x=1作为输入,y=0作为输出。
$$ \dfrac {\partial C} {\partial w} = (a-y)σ'(z)x =aσ'(z) $$
$$ \dfrac {\partial C} {\partial b} = (a-y)σ'(z) =aσ'(z) $$
然后更新w、b:
$$ w:= w-η \dfrac { \partial C} {\partial w} =w - η a *σ′(z) $$
$$ b:=b- η \dfrac { \partial C} {\partial b} =b - η a *σ′(z) $$
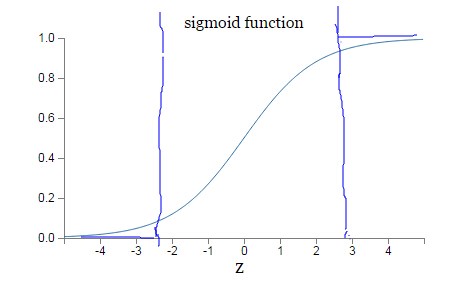
因为sigmoid函数的性质,导致σ′(z)在z取大值时会很小(如下图标出来的两端,几近于平坦),这样会使得w和b更新非常慢(因为η * a * σ′(z)这一项接近于0)。
交叉熵代价函数(cross-entropy cost function)
为了克服这个缺点,引入了交叉熵代价函数(下面的公式对应一个神经元,多输入单输出):
$$ C=- \dfrac 1 n \sum_x[ylna+(1-y)ln(1-a)] $$
其中y为期望的输出,a为神经元实际输出(a=σ(z), where $$ z=\sum_j w_jx_j + b $$ )
与方差代价函数一样,交叉熵代价函数同样有两个性质:
- 非负性(所以我们的目标就是最小化代价函数)。
- 当真实输出a与期望输出y接近的时候,代价函数接近于0.(比如y=0,a~0;y=1,a~1时,代价函数都接近0)。
另外,它可以克服方差代价函数更新权重过慢的问题。我们同样看看它的导数:
$$ \dfrac {\partial C} {\partial w_j}= \dfrac 1 n \sum_x x_j(σ(z)-y) $$
$$ \dfrac {\partial C} {\partial b}= \dfrac 1 n \sum_x(σ(z)-y) $$
可以看到,导数中没有σ′(z)这一项,权重的更新是受σ(z)-y这一项影响,即受误差的影响。所以当误差大的时候,权重更新就快,当误差小的时候,权重的更新就慢。这是一个很好的性质。