http://blog.csdn.net/taoyanqi8932/article/details/54409314
http://blog.csdn.net/u012374174/article/details/52885583
1.4.2 逻辑回归模型评估
1.由于逻辑回归是用来预测概率的,我们可以用AUC-ROC曲线以及混淆矩阵来确定其性能。
2.此外,在逻辑回归中类似于校正R2的指标是AIC。AIC是对模型系数数量惩罚模型的拟合度量。因此,我们更偏爱有最小AIC的模型。
3.空偏差指的是只有截距项的模型预测的响应。数值越低,模型越好。残余偏差表示由添加自变量的模型预测的响应。数值越低,模型越好。
查准率和查全率(Precision and Recall): 计算查准率与查全率实际上非常简单。想象一下在1万个案例中,有100个阳性案例。想要知道哪些是阳性案例,选出200个在其中选择,可以确保找到这100个阳性案例的机会更大。记录预测的ID,在拿到实际结果时,总结一下判断正确与错误的总次数。关于正确和错误共有四种判断方式:
TN(真阴性):本来是负样例的案例被分类成负样例。
TP(真阳性):本来是正样例的案例被分类成正样例。
FN(伪阳性):本来是正样例的案例,被错分成负样例,又称误报、误判。
FP(伪阴性):本来是负样例的案例,被错分成正样例,又称漏报、漏判。
| 预测为阴性 | 预测为阳性 | |
|---|---|---|
| 阴性案例 | TN:9760 | FP: 140 |
| 阳性案例 | FN:40 | TP: 60 |
预测的正确率是百分之多少? 你可以回答:“正确率”为1万分之(9,760+60),也就是98.2%。
查出的阳性案例占实际的多大比例(召回率)? 你可以回答:“查全率”是100分之60,也就是60%。
预测为阳性的案例正确率是多少? 你可以回答:“查准率”是200分之60,也就是30%。
ROC曲线表现了敏感性(查全率)与特异性(不准确)之间的关系,通常用于衡量二值分类器(binary classifiers)的性能。但是,在处理高度倾斜的数据集时,PR曲线(Precision-Recall)更能代表性能。可以参考Quora 的回答:ROC曲线和RP曲线之间的区别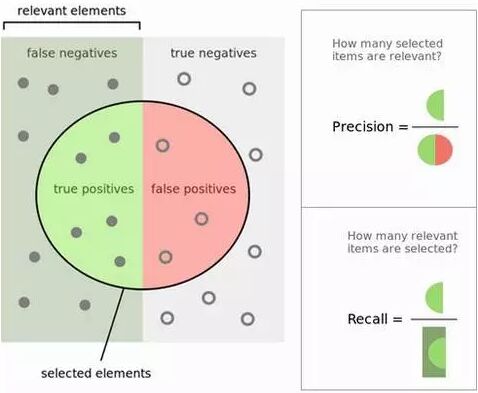
TP+FP+FN+FN:特征总数(样本总数)
TP+FN:实际正样本数
FP+TN:实际负样本数
TP+FP:预测结果为正样本的总数
TN+FN:预测结果为负样本的总数
有些绕,为做区分,可以这样记:相同的后缀(P或N)之和表示__预测__正样本/负样本总数,前缀加入T和F;实际样本总数的4个字母完全不同,含TP(正正得正)表示实际正样本,含FP(负正得负)表示实际负样本。
精度是确定分类器中断言为正样本的部分其实际中属于正样本的比例,精度越高则假的正例就越低,召回率则是被分类器正确预测的正样本的比例。两者是一对矛盾的度量,其可以合并成令一个度量,F1度量:
$$F1=\dfrac {2PR} {P+R}$$ (P是精准率,R是召回率)
PR(precision recall)曲线表现的是precision和recall之间的关系,如图所示:
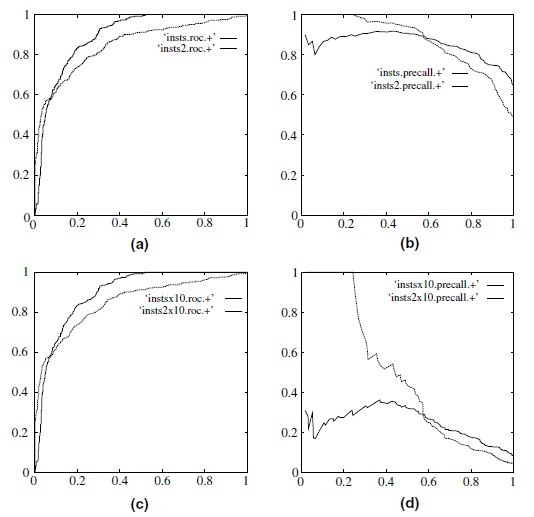
| ROC and precision-recall curves under class skew. (a) ROC curves, 1:1; (b) precision-recall curves, 1:1; (c) ROC curves, 1:10 and (d) precisionrecall |
|---|
如何选择ROC,PR
下面节选自:What is the difference between a ROC curve and a precision-recall curve? When should I use each?
Particularly, if true negative is not much valuable to the problem, or negative examples are abundant. Then, PR-curve is typically more appropriate. For example, if the class is highly imbalanced and positive samples are very rare, then use PR-curve. One example may be fraud detection, where non-fraud sample may be 10000 and fraud sample may be below 100.
In other cases, ROC curve will be more helpful.
其说明,如果是不平衡类,正样本的数目非常的稀有,而且很重要,比如说在诈骗交易的检测中,大部分的交易都是正常的,但是少量的非正常交易确很重要。
Let’s take an example of fraud detection problem where there are 100 frauds out of 2 million samples.
Algorithm 1: 90 relevant out of 100 identified
Algorithm 2: 90 relevant out of 1000 identified
Evidently, algorithm 1 is more preferable because it identified less number of false positive.
In the context of ROC curve,
Algorithm 1: TPR=90/100=0.9, FPR= 10/1,999,900=0.00000500025
Algorithm 2: TPR=90/100=0.9, FPR=910/1,999,900=0.00045502275
The FPR difference is 0.0004500225
For PR, Curve
Algorithm 1: precision=0.9, recall=0.9
Algorithm 2: Precision=90/1000=0.09, recall= 0.9
Precision difference= 0.81
可以看到在正样本非常少的情况下,PR表现的效果会更好。
如何绘制ROC曲线
为了绘制ROC曲线,则分类器应该能输出连续的值,比如在逻辑回归分类器中,其以概率的形式输出,可以设定阈值大于0.5为正样本,否则为负样本。因此设置不同的阈值就可以得到不同的ROC曲线中的点。
下面给出具体的实现过程:
来源:数据挖掘导论