3.1 协同过滤算法

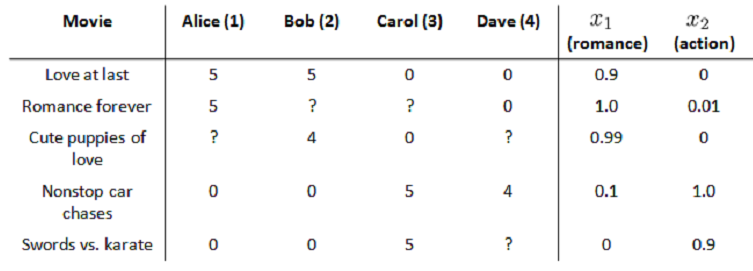
$$x_1 $$, $$x_2$$分别代表电影的浪漫程度和动作程度。每部电影都有一个特征向量，如$$x^{(1)}$$是第一部电影的特征向量[0.9,0]。

下面基于这些特征来构建一套推荐系统算法。

假设我们采用线性回归模型，我们可以针对每一个用户都训练一个线性回归模型，如$$ \theta^{(1)} $$是第一个用户的模型的参数。

于是，我们有：

• $$ \theta^{(j)} $$用户j的参数向量
• $$ x^{(i)} $$电影i的特征向量

对于用户j和电影i，我们的预测评分为：$$ (\theta^{(j)})^T(x^{(i)}) $$

代价函数

针对用户j，该线性回归模型的代价为预测误差的平方和，加上归一项：

$$ min{\theta^{(j)}} \dfrac 1 2 \sum{i:r(i,j)=1} ((\theta^{(j)})^Tx^{(i)}-y^{(i,j)} )^2 + \dfrac {\lambda} 2 \sum_{k=1}^n(\theta_k^{(j)})^2 $$

其中i:r(i,j)表示只计算那些用户j评过分的电影。为了学习所有用户，我们将所有用户的代价函数求和：

$$ min{\theta^{(1)}...\theta^{(n_u)}} \dfrac 1 2 \sum{j=1}^{nu}\sum{i:r(i,j)=1} ((\theta^{(j)})^Tx^{(i)}-y^{(i,j)} )^2 + \dfrac {\lambda} 2 \sum{j=1}^{n_u}\sum{k=1}^n(\theta_k^{(j)})^2 $$

然后用梯度下降法求解该公式。

协同过滤算法

如果我们既没有用户的参数，也没有电影的特征，用协同过滤算法可以同时学习这两者。

优化目标改成同时针对x和$$ \theta $$ 进行。$$ J(x^{(1)},...x^{(nm)}, \theta^{(1)},...\theta^{(n_u)}) =min{\theta^{(1)}...\theta^{(nu)}} \dfrac 1 2 \sum{j=1}^{nu}\sum{i:r(i,j)=1} ((\theta^{(j)})^Tx^{(i)}-y^{(i,j)} )^2 + \dfrac {\lambda} 2 \sum{i=1}^{n_m}\sum{k=1}^n(xk^{(j)})^2+\dfrac {\lambda} 2 \sum{j=1}^{nu}\sum{k=1}^n(\theta_k^{(j)})^2 $$对代价函数求偏导数

算法步骤如下：

1、初始化$$ x^{(1)}, x^{(2)}...x^{(nm)}, \theta^{(1)},...\theta^{(nu)} $$为一些随机小值。

2、使用梯度下降算法最小化代价函数

3、在训练完算法后，我们预测 $$ (\theta^{(j)})^T(x^{(i)}) $$为用户 j给电影 i 的评分

例如，如果一位用户正在观看电影x(i)，我们可以寻找另一部电影x(j)，依据两部电影的特征向量之间的距离||x(i)-x(j)||的大小。

均值归一化如果我们新增一个用户Eve，并且Eve没有为任何电影评分，那么我们以什么为依据为Eve推荐电影呢？

我们首先需要对结果Y 矩阵进行均值归一化处理，将每一个用户对某一部电影的评分减去所有用户对该电影评分的平均值：然后我们利用这个新的Y 矩阵来训练算法。

如果我们要用新训练出的算法来预测评分，则需要将平均值重新加回去，预测 $$ (\theta^{(j)})^T(x^{(i)}) +\mu_i $$

对于 Eve，我们的新模型会认为她给每部电影的评分都是该电影的平均分。